网络流总结 Ⅰ：概况 | 最大流

今天就来看看这些最大流板子里到底都是嘛玩意..

网络流

网络流 是图论中比较独立的一块，其算法基础不难，问题也相对具体，但编程复杂度不低，且其相关问题变化莫测、种类繁多，解题的难点往往在于对题目的抽象、转化与化归。因此需积累一定的题量和思考量，再加以总结，才可较为灵活地掌握这类算法问题。

网络流问题常见的求解目标有最大流（最小割）、最小费用最大流、上下界可行流等，我们逐一进行分析和总结。

最大流 / 最小割

最大流 / 最小割的概念很好理解，故在此不再赘述。另外由于最大流等于最小割，因此求最小割和求最大流实际上是同一个问题。

那么如何解决这个问题呢？我们主要有两类算法：增广类算法 和 预流推进类算法 。下面分别进行介绍：

一、增广类算法

思想分析

增广路算法的思想是，我不断地在网络中尝试从源点再发出一些流量，输往汇点，直至我无法再这样做。

首先我们定义残量网络是由原网络中仍然有未使用容量的弧构成的网络（初始时就是整个网络）。那么上述做法就是说，我不断地在残量网络中寻找一条从源到汇的通路，如果找到，记这条通路上所有弧中最少的未用容量值为 $r$，那么我就可以从源点再发出 $r$ 这么多流量输往汇点，这就叫一次增广，这条路就叫增广路。易见，每次增广后，该增广路就一定不再连通源汇了（未用容量最少的弧的剩余容量已被耗尽），因此我们需要再尝试增广其他的路。如果找不到，根据增广路定理，此时得到的流就是最大流。

增广路类算法有一个很重要的对称性是，建图时对于每条弧 $<u, v, c_0>$ 我都建一条反向弧 $<v, u, c_1>$，使他们成为一对相反弧（注意区分反向弧和相反弧的概念。反向弧是特指一批弧，即建图时反向建的弧，而相反弧是指和某条弧指向恰相反的弧。也就是说正向弧的相反弧是反向弧，反向弧的相反弧是正向弧）。

那么每次增广结束后，记此次增广了 $r$ 的流量，那么我们对于增广路上的每条弧，都需要将其相反弧的可用容量增加 $r$（注意到在这里也可能会对正向弧加容量，因为对于增广路上的反向弧，其相反弧就是正向弧）。这样相当于为后续提供了反悔的可能性，使我们总可以找到最大流。（正向弧流量-反向弧流量即为当前这对相反弧的净流量，其取正值表示净流量沿正向弧方向，取负值表示净流量沿反向弧方向）。

那么反向弧的初始容量 $c_1$ 取多少呢？注意到如果是有向图，那么净流量必须沿正向弧的方向，所以反悔最多也就只能把正向流量全部退回，因此反向弧的初始可用容量是 $c_1=0$，只有当正向弧有流量了，反向弧才有容量，且其值就等于正向弧当前已使用的流量；而如果是无向图，那么 $c_1=c_0$，因为净流量是可以取到 $[-c_0, c_0]$ 间的任意值的，所以一开始就可以往反向弧方向流。

算法实现

增广类算法的常见实现有：FF、EK(SAP)、Dinic、ISAP(SAP的GAP优化版)、 Bit-Scaling(Dinic的按位批量化优化版) 等。下面逐一进行介绍：

• $\text{FF}$：增广路算法的最朴素实现。在残量网络上不断 $\text{DFS}$ 找增广路，然后进行更新。对于整数容量网络，由于每次至少增广 $1$ 的流量，因此时间复杂度 $O(|max_{-}flow|)$。相对其他算法来说这是一个很糟糕的复杂度了，因此我们一般不使用此算法。

• $\text{EK(SAP, shortest augmenting path)}$：改进了一下 $\text{FF}$ 算法，用 $\text{BFS}$ 找增广路，并通过前驱数组进行更新。这样就保证每次都会按最短路（认为每条边距离都是单位 $1$）去增广。经证明可知其增广次数为 $O(VE)$ 的（详见算导。一个简要解释是，每条边成为限制当次增广流量的关键边的次数不会超过 $\text{V/2}$ 次，因为相邻两次成为关键边需要正着来一次和反悔来一次。记正着来之前 $dist[u]=a$，正着来一次后 $dist[v]$ 至少增成 $dist[u]+1=a+1$，再逆着来一次后 $dist[u]$ 就至少增成 $dist[v]+1=a+2$，所以每一对反悔操作都会让一条边的起点到源点距离至少增加 $2$，又因为距离最大不会超过点数，所以每条边最多成为 $\text{V/2}$ 次关键边，所以总共最多会有 $\text{E*V/2}$ 次关键边的出现，又因为每次增广至少消耗 $1$ 条关键边，所以最多增广 $\text{E*V/2}$ 次）。

  所以总时间复杂度是 $O(VE^2)$ 的。

• $\text{Dinic}$：在 $\text{EK}$ 基础上再进行优化。还是不断 $\text{BFS}$ 找增广路，但与此同时额外进行标记深度操作（称为构造层次图）。且待 $\text{BFS}$ 完成发现汇点可达后，用 $\text{DFS}$ 进行沿最短路的增广，而不是直接用前驱数组进行沿最短路的增广。

  易见，如果 $\text{Dinic}$ 也是每 $\text{BFS}$ 一次就 $\text{DFS}$ 一次，那还不如 $\text{EK}$ 直接用前驱数组来得方便。那 $\text{Dinic}$ 到底高在哪里呢？注意到我们的分层操作会把网络的拓扑结构保存起来，因此一次 $\text{BFS}$ 后其实是可以做多次增广的！因为 $\text{DFS}$ 不会破坏层次编号，所以我们在一次 $\text{BFS}$ 后可以一直 $\text{DFS}$ ，直到源汇不连通才进行下一次 $\text{BFS}$ 分层。这样效率就得到了提高。

  此外，$\text{Dinic}$ 还有两个更强的优化：当前弧优化 和 炸点优化，分别可以消除对不必要的弧和不必要的点的遍历。

  • 当前弧优化：可以说搞懂如何正确地做这个优化后，整个 $\text{Dinic}$ 的运作过程就彻底弄明白了。

    首先，什么叫当前弧优化？我们每次 $\text{DFS}$ 到某个点的时候，会按边的存储序依次访问其出边。如果能够确定其中前 $k$ 条边一定无法再增广，那么我这次就可以跳过这前 $k$ 条，从第 $k+1$ 条边进行这次增广。这就是当前弧优化。

    那么如何确定某条边无法再增广了呢？是不是它剩余容量为 $0$ 才说明无法增广？不。 这里有一个非常显而易见的反例（$a/b$ 表示总容量为 $b$，使用了 $a$）：
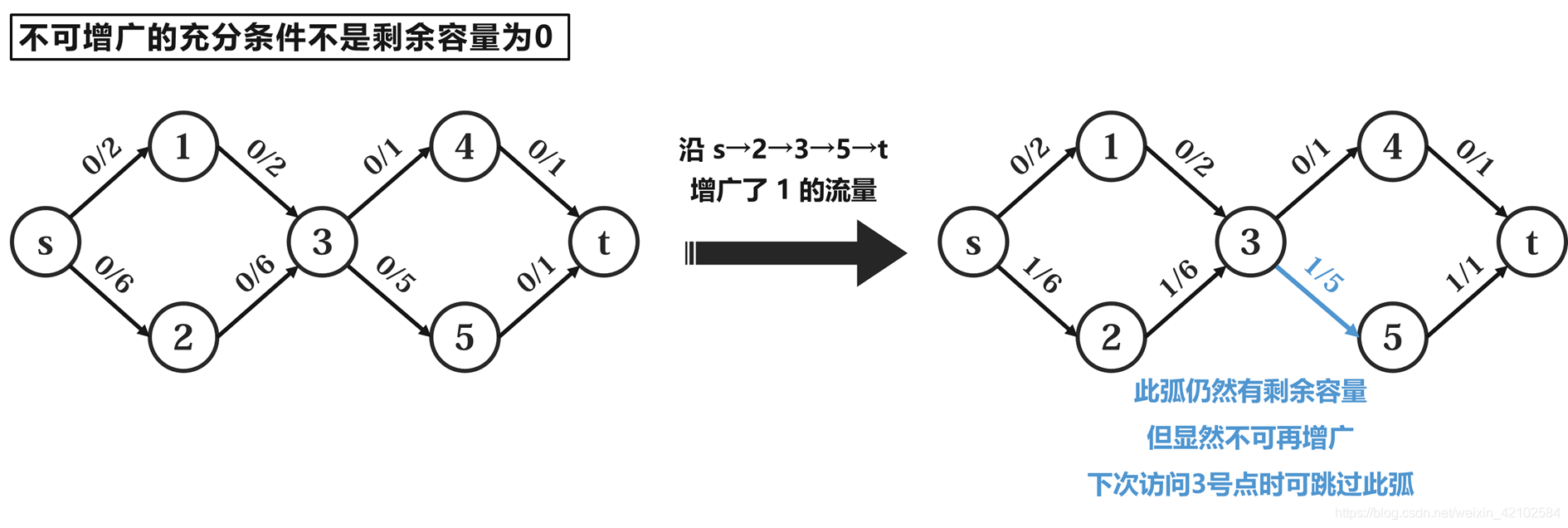
    那怎么判断？可以这样：如果曾经有 $>0$ 的流量 $f{in}$ 放在了它的起点，但在经过增广后 $f{in}$ 并没有全部用完，那么就说明这条弧不可能再增广更多了。如上图，当沿着 $s\rightarrow2\rightarrow3\rightarrow5\rightarrow t$ 这条路增广的时候，曾经就有 $6$ 这么多流量放在了 $3\rightarrow5$ 的起点 $3$ 这里，然而最多只能沿这条弧流出 $1$。因此如果以后再访问到 $3$ 号点，$3\rightarrow5$ 这条弧就可以不看了。

    【注意】 是曾经增广过且流量没用完才能跳过，而不是只要曾经增广过就能跳过！曾经增广过且耗尽了输入流量时，我们并不能跳过这条边，因为他可能还有增广的潜力（只是这次的流量输入不够所以只能增广这么多了，下次再来流量还可以再增广）。我们再举一个例子：
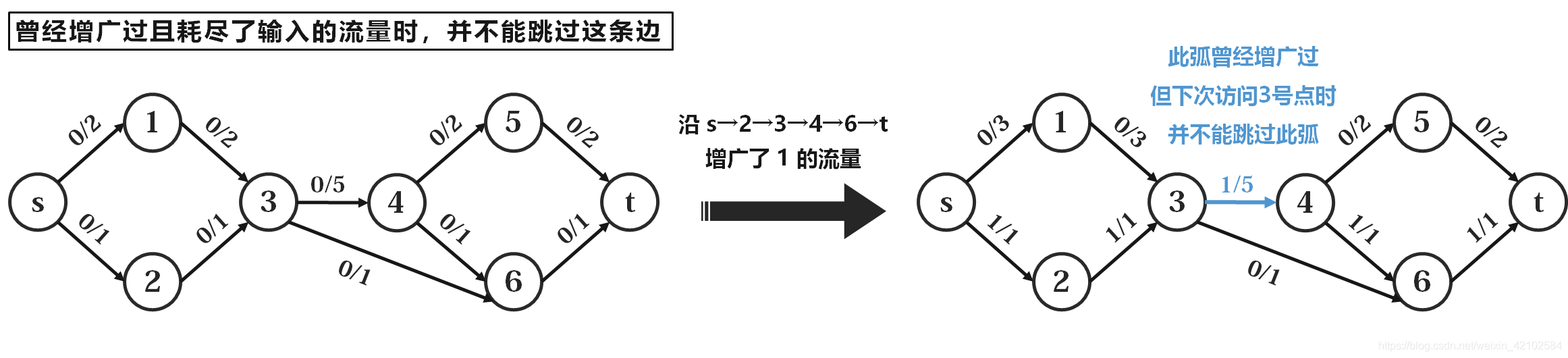
    如沿上图路径增广的时候，曾经有 $1$ 这么多流量放在了 $3\rightarrow4$ 的起点 $3$ 这里，然后流出了 $1$。显然，如果以后再访问到 $3$ 号点，我们并不能跳过 $3\rightarrow4$ 这条弧。比如下一次可以沿 $s\rightarrow1\rightarrow3\rightarrow4\rightarrow5\rightarrow t$ 这条路增广 $2$ 的流量。

    所以这个地方一定要注意编程细节（可详见后续代码部分），否则稍不留神就会写错代码，使得当前弧优化变成当前弧劣化。

  • 炸点优化：名字倒是挺凶的... qwq

    其实就是在 $\text{DFS}$ 的过程中，如果遍历到了 $u$ 这个点的某条出边（记其指向 $v$ 这个点），且从这条边 $\text{DFS}$ 回来后发现一点流量都没有增广，就说明这棵子树的枝节全部都是盲端。那么就可以把 $v$ 为根的这棵子树全部炸掉（把这些点的层数编号设为一个负数，使得在下一次重新分层前他们就不会再被访问到了）

  这就是 $\text{Dinic}$ 了，可以说它是求最大流最常用的算法了。后面会贴出其详细代码，其中的当前弧优化部分一定要仔细理清思绪。这样才能真正理顺此算法的流程，避免编写代码时翻车。

  另外，经证明 $\text{Dinic}$ 的复杂度可达 $O(V^2E)$，面对一般的网络流问题已足矣。

• $\text{I SAP}$：

代码

• Dinic：

template <const bool directed, typename cint>
class Dinic
{
private:

    static constexpr auto CINT_MAX = std::numeric_limits<cint>::max();

    struct Ed   // 链式前向星。由于存在异或找反边的trick，使用下标式而不是指针式。（就算存指向反边的指针也不如异或快，实测）
    {
        int ne, v;
        cint c;
    } ed[ME];
    int head[MV], cur[MV], tot;
    int V, S, T;

    int de[MV];
    bool bfs()
    {
        static int q[MV];
        int hd = 0, tl = 0;

        memset(de, 0, sizeof(*de) * (V+2));
        de[q[tl++]=S] = 1;
        while (hd != tl)
        {
            const int u = q[hd++];
            for (int i=head[u]; i; i=ed[i].ne)
            {
                const int v = ed[i].v;
                if (ed[i].c && !de[v])
                {
                    de[q[tl++]=v] = de[u] + 1;
                    if (v == T)
                        return true;
                }
            }
        }

        return false;
    }

    cint dfs(const int u, cint in)  // 进dfs时，保证in一定 > 0
    {
        if (u == T)
            return in;
        cint out = 0;

        /* 【当前弧优化】：跳过一定无法再增广的边。
            什么时候可以认为一条边一定无法再增广了？就是曾经有>0的in流量放在了它的起点，但在经过增广后in流量并没有用完。这就说明它不可能再增广更多了。
            因此for循环每进行一次（相当于榨干了一条边的增广潜力），我们就可以更新一次cur[u]，直到in用完或者已经遍历完u的一切出边了。
            所以要注意最后一次循环到底是怎么退出的：
            1. (in==0 && i!=0) || (in==0 && i==0)：
                假设最后一次循环内这条边叫ed[i0]。ed[i0].ne==i1。那么ed[i0]可能是仍然能增广的（这次是因为in没了才没增广成功的，如果再给一些in，可能还可以增广）
                那么退出for之后cur[u]应该是多少？显然应该是i0（因为ed[i0]可能还有潜力，跳过他就可能错过了，就失去了优化效果。）。
                所以我们不能把for循环写成下面三种样子（他们是互相等价的）：（写成这样的话退出循环后cur[u]就会是i1了）
                    a) for (int i=cur[u]; i&&in; cur[u]=i=ed[i].ne)
                    b) for (int &i=cur[u]; i&&in; i=ed[i].ne)（和a写法完全等价）
                    c) for (int i=cur[u]; (cur[u]=i) && in; i=ed[i].ne)（和a写法相比只是在进入循环时多了一次没用的赋值）
                但是这样可以：（刚好利用了&&的短路性质，使得for循环因为in==0退出时，cur[u]不会被更新成i1）
                    d) for (int i=cur[u]; in && (cur[u]=i); i=ed[i].ne)
                或者我们把in==0时跳出的这句话给移出for的第二部分，移到for循环体内，那还是可以用以上三种写法的（特别是引用，这个最方便）。
            2. in!=0 && i==0：
                只有这种情况才可以把cur[u]更新成i2，且此时i2刚好是0。

            所以到底怎么写当前弧优化呢？上面有一种利用&&短路性质的写法。除了这种，更常见的写法是在for循环体里面写。
            那么写在哪？只要写在if外面都能起到及时更新而又不会在in==0时误更新的效果（不用担心写在for循环体最后会导致更新不及时。因为中间的递归过程里不可能再经过u这个点（因为一直是按dep的严格增序dfs的））
            而最好不要写在if里面。不能说这条边没进if就不更新了。实际上如果这条边连再向下dfs都不行的话，更说明他无法再增广了。

            但是这些在for里面写的写法有极为轻微的性能降低，因为他们绝对不会在循环结束的那次进行更新。
            所以如果循环结束时in!=0而i==0，他们就没更新，而实际上这种情况是可以把cur[u]更新成i（也就是0）的。因为in流量还有剩余，说明u发出的所有边都一定不能再增广了

            不过可以通过在最后炸点的时候把in!=0的点也炸掉来弥补这个微弱的性能降低 
        */
        for (int i=cur[u]; in&&(cur[u]=i); i=ed[i].ne)              // 【判in优化】：剪枝
        {
            if (ed[i].c>0 && de[ed[i].v]==de[u]+1)
            {
                const cint tp = dfs(ed[i].v, MIN(in, ed[i].c));     // 【多路增广优化】：一次bfs分层，多次增广。
                in -= tp, out += tp, ed[i].c -= tp, ed[i^1].c += tp;
            }
        }

        // 因为进函数时in必>0，所以退出函数前若in==0则out必!=0，而in!=0时out可能为0（没增广或者增广了0）可能不为0，out==0时in可能为0（in耗尽）也可能不为0（没耗尽）
        // 所以if的两个条件并不是包含关系，因此不用担心某个条件是多余的
        if (in || !out) // in不等于0就退出了for，说明u的所有出边都无法再增广；out==0则显然是增广失败的标志。
            de[u] = -1; // 【炸点优化】：此路不通，剪掉盲枝
        return out;
    }

public:

    void init(const int v)
    {
        memset(head, 0, sizeof(*head) * (V+2)); // 注意是清V+2个，不是清v+2个。这样第一次就只会清2个。
        V = v;
        tot = 1;    // 不是2，如果tot是2那第一条边就是3了... 要让第一条边是非0偶数才行
    }

    void edd(const int u, const int v, const cint c = CINT_MAX) // 不填容量就是加无穷大容量
    {
        ed[++tot].ne=head[u], ed[tot].v=v, ed[tot].c=c, head[u]=tot;
        ed[++tot].ne=head[v], ed[tot].v=u, ed[tot].c=directed ? 0:c, head[v]=tot;   // 单向:ed[tot].c=0; 双向:ed[tot].c=c
    }

    cint max_flow(const int s, const int t)
    {
        cint sum = 0;
        S = s, T = t;
        while (bfs())
        {
            memcpy(cur, head, sizeof(*head) * (V+2));
            sum += dfs(s, CINT_MAX);
        }
        return sum;
    }
};

后文链接

• 1
• 2